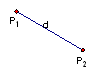
 Afstand mellem to punkter,
`P_1(x_1,y_1)` og `P_2(x_2,y_2)`
Afstand mellem to punkter,
`P_1(x_1,y_1)` og `P_2(x_2,y_2)``dist(P_1,P_2)=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`
Vi har to afstandsformler
 Afstand mellem to punkter,
`P_1(x_1,y_1)` og `P_2(x_2,y_2)`
Afstand mellem to punkter,
`P_1(x_1,y_1)` og `P_2(x_2,y_2)`
`dist(P_1,P_2)=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`
Eksempel: Vi vil beregne afstanden mellem punkterne `A(-2,3)`
og `B(4,-1)`
`dist(A,B)=sqrt((4-(-2))^2+(-1-3)^2)=sqrt(52)`
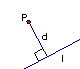 Afstand fra punkt,
`P(x_1,y_1)` , til linje `l:y=ax+b`
Afstand fra punkt,
`P(x_1,y_1)` , til linje `l:y=ax+b`
`dist(P,l)=|y_1-(a*x_1+b)|/sqrt(1+a^2)`
Eksempel: Vi vil beregne afstanden fra punktet `P(-2,3)`
til linjen `l:y=-3x+4`
`dist(P.l)=|3-(-3*(-2)+4)|/sqrt(1+(-3)^2)=7/sqrt(10)`
Hvis linjens ligning er få form `ax+by=c` kan man som regel isolere y og anvende afstandsformlen ovenfor.
Hvis der ikke er nogen y-er, kan man ikke isolere y, men så kan man isolere x.
Eksempel: Afstanden fra punktet `P(2,-3)` til linjen med
ligning `x=5`
er her slet og ret forskellen mellem x-værdierne, dvs `|5-2|=3`
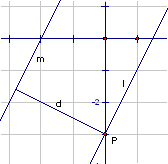 Afstanden mellem to
linjer (defineret som den korteste afstand mellem et punkt på den ene linje
og et punkt på den anden linje) er normal 0, idet linjernes skærings ligger på
begge linjer.
Afstanden mellem to
linjer (defineret som den korteste afstand mellem et punkt på den ene linje
og et punkt på den anden linje) er normal 0, idet linjernes skærings ligger på
begge linjer.
Hvis linjerne er parallelle, kan den vinkelrette og mindste afstand beregnes ved
at vælge et punkt på den ene linje og bruge afstandsformlen fra dette punkt til
den anden linje.
Eksempel: Find afstanden mellem linjerne `l:y=2x-3` og `m:y=2x+4`
Vi skal finde et punkt på for eksempel l: med `x=0` indsat i
ligningen fås `y=-3` så punktet `P(0,-3)` ligger på l.
Herefter beregnes den søgte afstand med
`dist(P,m)=|-3-(2*0+4)|/sqrt(1+2^2)=7/sqrt(5)`
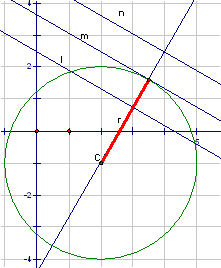 Afstand (den korteste)
mellem linje og cirkel
Afstand (den korteste)
mellem linje og cirkel
Hvis afstanden fra cirklens centrum, C, til linjen, l, er mindre en cirklens
radius
`dist(C.l)<r`
så skærer linjen cirklen, og afstanden er 0.
Hvis afstanden fra cirklens centrum, C, til linjen, m, er lig med cirklens
radius
`dist(C.m)=r`
så rører linjen cirklen (tangerer), og afstanden er 0.
Hvis afstanden fra cirklens centrum, C, til linjen, n, er større end cirklens
radius
`dist(C,n)>r`
så er afstanden fra linjen hen til cirklen lig med hele afstanden ind til
centrum minus cirklens radius
`dist(n,cirkel)=dist(n,C)-r`
Afstand (den korteste) mellem to cirkler
Hvis cirklerne skærer hinanden, er afstanden 0.
Hvis cirklerne ikke skærer hinanden, kan afstanden udtrykkes som afstanden
mellem cirklernes centrer plus eller minus deres radier, alt efter beliggenhed.
Eksempel:
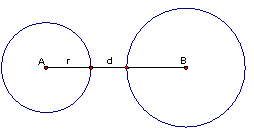 Hvis cirklerne ligger som vist på
figuren, kan afstanden, d, mellem cirklerne beregnes som
Hvis cirklerne ligger som vist på
figuren, kan afstanden, d, mellem cirklerne beregnes som
`dist(A,B)-r-R`
Eksempel:
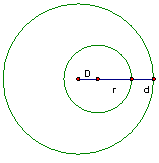 Hvis cirklerne ligger som på
figuren med radier r og R, indbyrdes afstand d og centerafstand D, har vi
Hvis cirklerne ligger som på
figuren med radier r og R, indbyrdes afstand d og centerafstand D, har vi
`R=D+r+d` hvoraf
`d=R-r-D`
hvor centerafstanden beregnes som afstanden mellem to punkter - de to centrer.